Es wird ein Geometriemodell vorgestellt, das ressourcensparend übertragen und gespeichert werden kann. Bei vollständiger Integration in die einschlägigen Anwendungen kann es an die Stelle der technischen Zeichnung treten bzw. die Integration der Anwendungen wesentlich verbessern. Das neue Geometriemodell ist so konzipiert, daß es per "Geometriedatenbus" aus einer anwendungsunab-hängigen Datenbasis verteilt und betreut wird. Der Geometriedatenbus besteht aus der Geometrieverteilung und einem integrierten Geometrie-Veränderungsservice. Die interaktive Geometriedarstellung auf graphischen Bildschirmen wird durch den Geometriedatenbus zur eigenständigen Anwendung; der 3D-Geometrieserver ermöglicht bei voller Ausnutzung der Bildschirm-Funktionalitäten ergonomisch optimale 3D-Manipulation. Mit dem 3D-Geometrieserver werden die funktionalen Begrenzungen der X-Window-Technik bezüglich der 3D-Geometrie-Verarbeitung überwunden.

2. Einleitung

Trotz hochentwickelter und rechnergestützter Konstruktionssysteme ist die technische Zeichnung häufig noch die verbindliche, Bauteile beschreibende Geometrieinformation. So verwundert es nicht, daß selbst hochentwickelte Konstruktionssysteme Funktionen zur Ausgabe von technischen Zeichnungen besitzen. Viele moderne Flugzeuge sind auf mikroverfilmten Konstruktionszeichnungen dokumentiert. In den folgenden Kapiteln wird ein Geometriemodell vorgestellt, das bei konsequenter Anwendung die volle Geometriedokumentation von Flugzeugen und ähnlich komplexen Geräten übernehmen kann.

3. Das einheitliche Geometriemodell

Die lückenlose und genaue Beschreibung der Oberfläche von Bauteilen ist die Hauptanforderung an ein einheitliches Geometriemodell. Nur mit Flächendarstellungen, die an jedem Punkt die Berechnung einer genauen Normalenrichtung erlauben, lassen sich Anforderungen wie die hochwertige graphische Darstellung (shaded image) und die automatisierter Fertigung (numerical control) befriedigen. Mit Flächen lassen sich alle zur zeichnerischen Darstellung notwendigen Kanten und Umrisse funktional verknüpfen. Von Flächen lassen sich (ggf. mittels gespeicherter Polyedrisierungs-Algorithmen mit wählbarer Toleranz) Elemente für Vielflach-Geomerie (solids) generieren wie sie für Kollisions- und Einbau-Untersuchungen benötigt werden.

3.1 Parametrische Geometrie

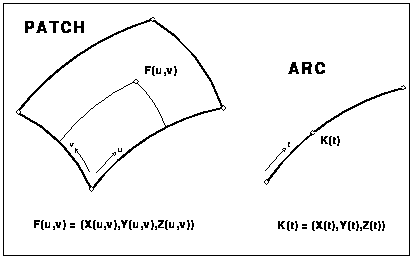
Das hier gezeigte Geometriemodell soll hauptsächlich die vollständige Hülle von Bauteilen - "die Grenze zwischen Material und Luft" - darstellen. Die Basis des Geometriemodells sind parametrische Flächen (PATCH), Kurven (ARC) und Punkte (POINT).

Flächen werden mit

Kurven mit

definiert (Bild 1).
 

Neben der vollständigen Flächenbeschreibung mittels Daten sind auch Flächen möglich, die von Kurven und Flächen abhängen (Bild 2).

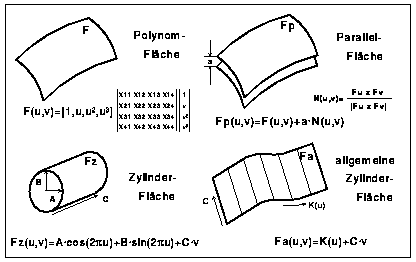
Kurven können als Raumkurve, als Kurve auf einer Fläche oder als Kurve auf einer Kurve definiert werden (Bild 3).

Punkte können als Raumpunkte, als Punkte auf einer Fläche oder als Punkte auf einer Kurve definiert werden (Bild 4).
 

Diese Art der Punktdefinition erlaubt die Relation von Aerodynamik- und Statik-Modellen mit der Bauteil-Geometrie.

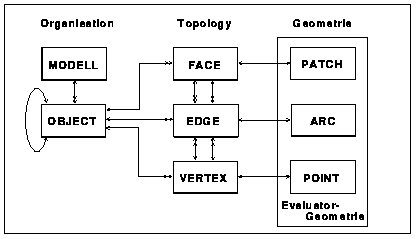
3.2 Verknüpfende Topololog

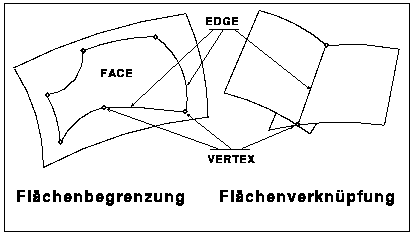
Zur vollständigen Beschreibung der Bauteiloberfläche muß aus den Flächen (PATCH) per Flächenbegrenzung der Teil herausgeschnitten werden, der zum Bauteil gehört (FACE). Jede Flächenbegrenzung ist über eine Kantenbeziehung (EDGE) mit einer Flächenbegrenzung auf der Nachbarfläche verknüpft. Die Kanten selbst sind mittels der Kantenendpunktbeziehung (VERTEX) mit anderen Kanten verknüpft (Bild 5).
 

3.3 Evaluatortechnik

Mittels einer Evaluatortechnik ist es möglich alle in Konstuktionssystemen vorkommenden Flächenbeschreibungen ohne Umwandlung zu integrieren. Ein Evaluator ist ein Programm, das für gegebene Flächenparameter (u,v) den Flächenpunkt (x,y,z) und bei Bedarf Ableitungen berechnet. Entsprechendes wird von einem Kurvenevaluator für einen Kurvenparameter (t) berechnet. Die Evaluatortechnik erlaubt, Speicherplatz und Übertragungskapazität sparende Funktionen (z.B. trigonometrische) zu integrieren, die bis zu 98% weniger Speicherplatz gegenüber Polynomgeometrie benötigen (Bild 6).
 

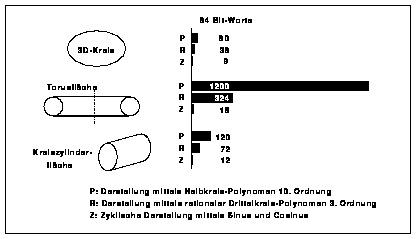
Natürliche Konstruktionsmerkmale wie Ebenheit, Zylinderform oder Rotationsgeometrie sind den Evaluatoren eingeprägt und müssen daher nicht durch Analyse der Flächengeometrie mühsam ermittelt werden. Die Evaluatortechnik bietet eine einheitliche Schnittstelle für alle einschlägigen Anwendungen. Die Evaluatortechnik erlaubt die funktionale Verknüpfung von Punkten, Kurven und Flächen auch verschiedener Objekte.

3.4 Modellstrukturierung durch Objekte

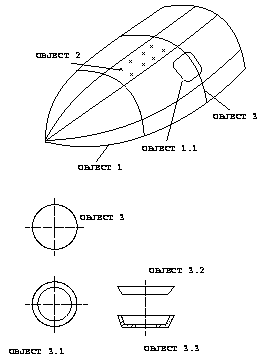
Zur Untergliederung des Geometriemodells werden die oben definierten Elemente in Objekten gesammelt (Bild 7).

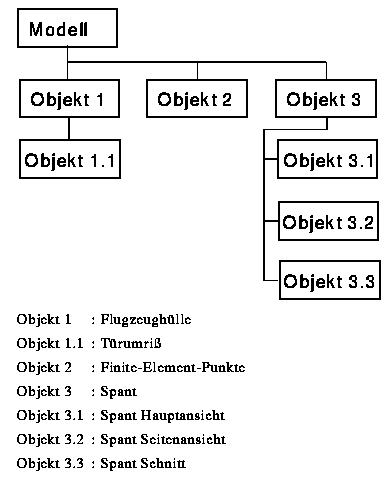
Eine mögliche Objektkollektion zeigt Bild 8. Das dabei gezeigte Finite-Element-Objekt dient in erster Linie der Punktabgriff-Dokumentation. Die Weiterentwicklung zu einem kompletten Finite-Element-Objekt ist denkbar.

3.5 Geometrie-Datenbank

Die Menge der für ein komplexes Gerät zu speichernden Informationen und die Notwendigkeit, Untermengen z.B. Bauteilgeometrien unabhängig zu verteilen, macht eine Zweiteilung der Datenbank in Modellverwaltung und portierbare Einzelmodelle notwendig. In der Modellverwaltung werden zweckmäßigerweise Informationen wie Gewicht, Schwerpunkt, Lage, und räumliche Ausdehnung gespeichert. Weitere zentral abzulegende Informationen sind Passungspaarungen, Montageflächen u.s.w. Auch die für die Portierbarkeit von Einzelmodellen notwendigen Kopien von Geometrie (z.b. Flugzeughüllenelemente) können und müssen mit Rücksicht auf Änderungsdienst zentral in der Modellverwaltung vermerkt werden. Die portierbaren Einzelmodelle erhalten im Fall der Strakgeometrie ein auf die notwendigen Flächen abgemagertes Strak-Objekt.

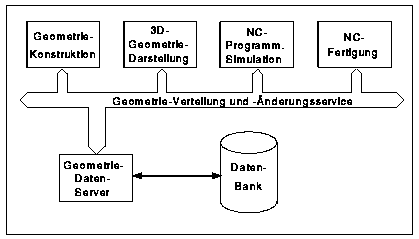
4. Geometrieverteilung per Datenbus

Bei der Betrachtung der heutigen Rechner-gestützten Systeme mit Geometrieverarbeitung fällt auf, daß mit Zunahme des 3D-Geometrieanteils mehr und mehr die verteilte Verarbeitung auf X11-Terminals verlassen wird und Workstation-Lösungen angeboten werden. Der Grund liegt in der in der hohen Netzbelastung und der Reaktionsträgheit bei echten 3D-Geometriemanipulationen, da das X11-Konzept alle Benutzereingaben über das Netzwerk leiten muß.

Das Konzept eines einheitlichen Ingenieur-Arbeitsplatzes müßte bei zunehmenden 3D-Geometrieanteil unter diesen Umständen verlassen werden. Abhilfe bringt die konsequente Einführung eines einheitlichen Geometriemodells, die Aufteilung der Geometrie-verarbeitenden Systeme in getrennte Verarbeitungs-, Darstellungs- und Speicherungssysteme und der Geometriedatenbus. Der Geometriedatenbus verbindet bei mäßiger Netzbelastung Anwendungsprogramme (z.B Konstruktion, NC-Programmierung, NC-Simulation, Einbauuntersuchung, NC-Fertigung) und den Darstellungs-Prozess (siehe Kap. 5.) mit dem 3D-Geometrieserver (siehe Kap. 6.). Aktive Geometrie-erzeugende Anwendungsprogramme haben dabei die Aufgabe dem Geometrieserver Modellveränderungen zu melden, der für die Speicherung und Verteilung sorgt.
 

5. Interaktive 3D-Geometriedarstellung

Die Herauslösung des Darstellungsprozesses aus den Anwendungsprogrammen hat den Zweck, daß einerseits das Anwendungsprogramm von der Aufgabe der Geometriedarstellung entlastet wird und anderseits der Display optimal gestaltet werden kann. Während Anwendungsprogramme bei der Darstellung der Modellgeometrie diese in einzelne Teile zerlegt quasi eindimensional per Interface-Standards (Phigs, Phigs++, graPhigs, GL,...) an den Display weiterleiten müssen, kann eine auf einem einheitlichen Geometriemodell aufsetzende graphische Spezialeinheit alle Möglichkeiten der Parallelverarbeitung ohne Standard-Display-Schnittstelle ausnützen. Die Netzbelastung für die Geometriedarstellung bleibt gering, weil neben der Einmalübertragung des Geometriemodells nur die Veränderungen übertragen werden müssen. Der Hauptvorteil besteht darin, daß alle graphischen Geometriemanipulationen örtlich erfolgen und einheitlich für alle Anwendungen durchgeführt werden. Als X11-Terminal unterstützt diese graphische Spezialeinheit die Anwendungsprogramme durch die Ausgabe der Menues.

6. 3D-Geometrieserver

Der Geometrieserver ist Quelle und Empfänger der Geometriedaten. Aktive Geometrieerzeuger wickeln alle Geometriemanipulationen wie Erzeugung, Veränderung und Löschung über den Geometrieserver ab. Der Geometrieserver selbst übermittelt alle Geometriemanipulationen an die beteiligten passive Prozesse wie 3D-Darstellung und zentraler Geometrieverwaltung. Auf diese Weise wird auch eine absturzsichere weil verteilte Geometriespeicherung erreicht. Teile des Geometrieservers können auf der Recheneinheit des Geometrieerzeugers geladen sein, um den Geometriezugriff so effizient wie möglich zu gestalten. Die Verteilung der Geometriemodelle erfolgt in binärer Form, wobei die Umwandlung der Daten in die jeweilige rechnereigene binäre Form Bestandteil des Übertragungsprotokolles ist.

7. Zusammenfassung

Das vorgestellte Konzept ist in wesentlichen Teilen durch Prototyparbeiten verifiziert. Die zunehmende Verteilung und Vernetzung der am Geometrieerstellungsprozess beteiligten Personen und Gruppen (z.B. Heimarbeitsplatz) wird stark von Speicherplatz- und Datenübertragungskosten beeinflußt. Der auf ca. 10% reduzierbare Modellumfang bei Evaluatortechnik gegenüber Polynomgeometrie schafft Reserven für komplexe Anwendungen wie das elektronische Gesammtanschauungsmodell (mockup) von Flugzeugen. Die vorgestellte Geometriemodelltechnik kann im Rahmen der weltweiten STEP-Standardisierung als hochinteraktive Lösung eingesetzt werden.

8. Schrifttum

Faux, I.D. and Pratt, M.J. (1981), Computational Geometry for Design and Manufacture, Ellis Horwood limited Publishers Chichester

Rembold, U. and Dillmann, R. (1986), Computer-Aided Design and Manufacturing, Springer-Verlag, Berlin

Eckert, H. (1988), Anforderungen der Fertigung an ein rechnerinternes CAD-Modell, VDI Bildungswerk BW8834